Các bước để tìm tập xác định hàm số mũ logarit
Tìm tập xác định của hàm số mũ logarit là một bước cơ bản nhưng quan trọng. Đây là một dạng toán trong chương trình Toán lớp 11. Các bước để tìm tập xác định dạng này như thế nào.
Các bạn nên làm theo những bước sau:
- Bước 1: Xác định các thành phần cần tìm điều kiện xác định: logarit, biểu thức chứa căn, phân số, biểu thức có mũ
- Bước 2: Tìm điều kiện của từng thành phần
- Bước 3: Kết hợp các điều kiện
- Bước 4: Kết luận
Đây là 4 bước cơ bản để tìm điều kiện xác định hàm số mũ-logarit. Nhìn chung, những bước này tương đối dễ nhớ. Do đó, các bạn cần thực hành thật nhiều để thành thục những bước biến đổi cơ bản. Với những bài tập tìm điều kiện xác định chỉ là một phần nhỏ thì bỏ qua bước 4.
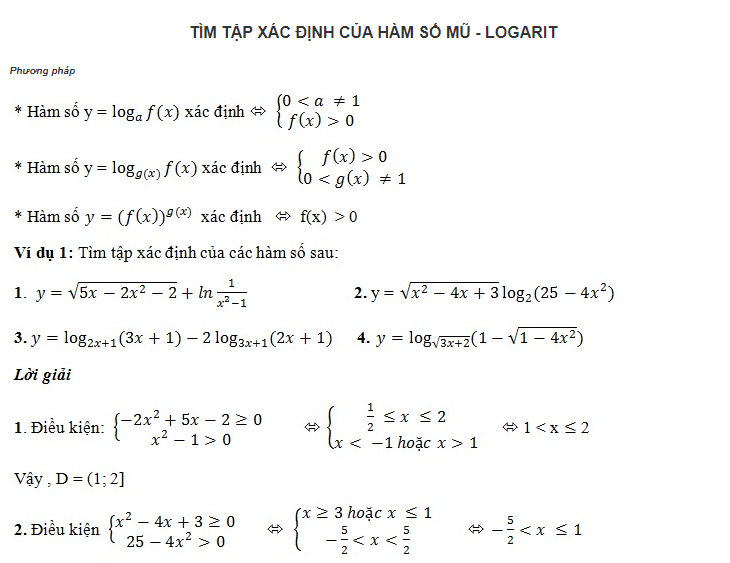

Kết hợp điều kiện bằng trục số
Trong những bài tập tìm tập xác định của hàm số mũ-logarit, với bài nhiều điều kiện thì có thể gây khó khăn cho học sinh. Các bạn rất khó khi nhìn nhiều biểu thức chứa dấu > < rồi kết hợp. Có một phương pháp rất dễ thực hiện mà kết quả luôn đúng. Đó là sử dụng trục số.
Các bước thực hiện phương pháp này như sau:
- Bước 1: Tìm các khoảng giá trị cần kết hợp
- Bước 2: Biểu diễn các khoảng giá trị trên trục số
- Bước 3: Tùy thuộc vào trường hợp lấy “hoặc” hay “và” mà gạch bỏ những phần không phù hợp.
- Bước 4: Kết luận
Phương pháp này có thể áp dụng khi có từ hai khoảng cần kết hợp trở lên. Khi làm quen các bạn sẽ thấy phương pháp này rất hữu ích. Nó giúp các bạn kết hợp nhanh và chính xác hơn bao giờ hết. Chúc các bạn học tốt!
Sưu tầm: Trần Thị Nhung
