Kiến thức cần nhớ về tiếp tuyến của đồ thị.
Chỉ còn vài tháng nữa thôi là các bạn học sinh lớp 12 bước vào kì thi quan trọng là kì thi THPT QG. Trong kì thi, một trong những kiến thức quan trọng các bạn cần ôn luyện vững chắc. Đó là phương trình tiếp tuyến của đồ thị. Để viết được một phương trình tiếp tuyến của đồ thị thì cần phải biết được hệ số góc của tiếp tuyến và toạ độ của tiếp điểm.
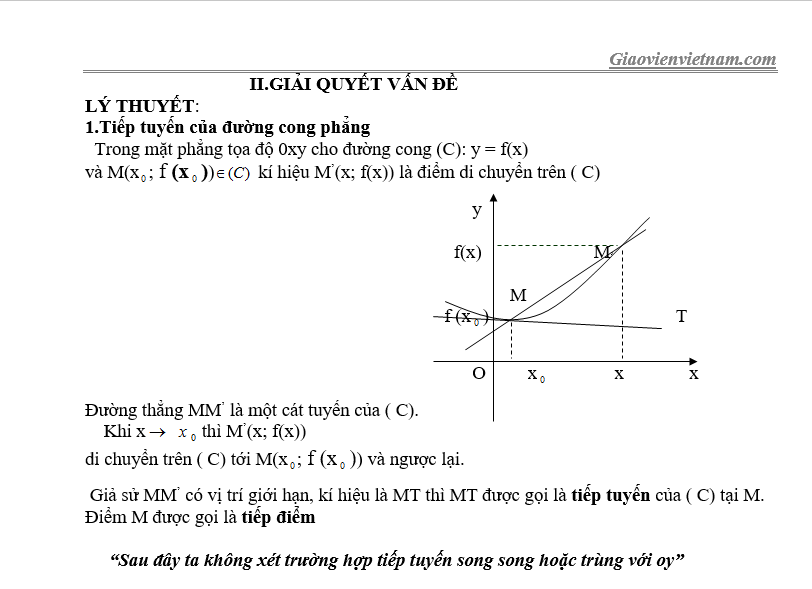
Giả sử: Biết toạ độ của tiếp điểm là A(x0; y0) và hệ số góc tiếp tuyến là k = f’(x0). Suy ra ta có phương trình tiếp tuyến của đồ thị (C) tại điểm A(x0; y0) là:
d: y = f’(x).(x – x0) + y0
Trong đó, Hệ số góc của tiếp tuyến là hệ số của góc tạo thành khi đường thẳng (d) cắt trục hoành x0Ox tại một điểm hoành độ hợp với trục hoành x0Ox tạo thành một góc.
- f’(x) > 0 tạo góc nhọn và nằm bên trái Oy.
- f’(x) < 0 tạo góc tù và nằm bên phải Oy
- f’(x) = 0 thì đường thẳng song song với trục hoành => không có hệ số góc.
Các dạng bài tập liên quan đến hệ số góc của tiếp tuyến
Trong chuyên đề về tiếp tuyến, các bạn được làm quen với các dạng bài sau:
- Dạng 1: Viết PTTT của đồ thị HS (C): y = f(x) tại A(x0; y0)
- Dạng 2: Viết PTTT của đồ thị HS (C): y = f(x) có hệ số góc k cho trước.
- Dạng 3: Viết PTTT của đồ thị HS (C): y = f(x) biết tiếp tuyến đi qua A(x1; y1)
- Dạng 4: Viết PTTT chung của hai đồ thị HS (C1): y = f(x) và (C2) y = g(x)
Để nắm vững được các dạng, các bạn cần làm bài tập thật nhiều. Hãy tham khảo tài liệu bên dưới để có nhiều bài tập rèn luyện
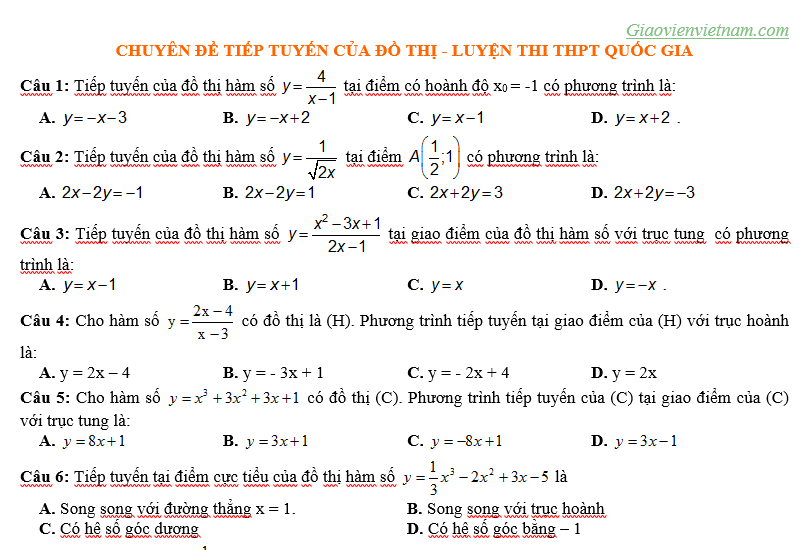
Sưu tầm: Thu Hoài
